


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 7-8-2019
Date: 16-8-2018
Date: 16-8-2019
|
An approximation for the gamma function 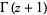 with
with ![R[z]>0](http://mathworld.wolfram.com/images/equations/LanczosApproximation/Inline2.gif) is given by
is given by
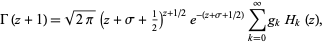 |
(1) |
where 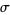 is an arbitrary constant such that
is an arbitrary constant such that ![R[z+sigma+1/2]>0](http://mathworld.wolfram.com/images/equations/LanczosApproximation/Inline4.gif) ,
,
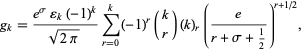 |
(2) |
where 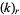 is a Pochhammer symbol and
is a Pochhammer symbol and
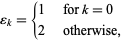 |
(3) |
and
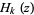 |
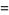 |
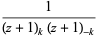 |
(4) |
 |
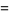 |
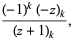 |
(5) |
with 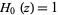 (Lanczos 1964; Luke 1969, p. 30).
(Lanczos 1964; Luke 1969, p. 30). 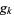 satisfies
satisfies
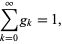 |
(6) |
and if 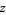 is a positive integer, then
is a positive integer, then 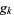 satisfies the identity
satisfies the identity
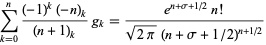 |
(7) |
(Luke 1969, p. 30).
A similar result is given by
![ln[Gamma(z)]](http://mathworld.wolfram.com/images/equations/LanczosApproximation/Inline16.gif) |
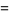 |
![(z-1/2)lnz-z+1/2ln(2pi)+1/2[(c_1)/(z+1)+(c_2)/(2(z+1)(z+2))+...]](http://mathworld.wolfram.com/images/equations/LanczosApproximation/Inline18.gif) |
(8) |
 |
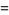 |
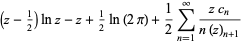 |
(9) |
 |
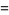 |
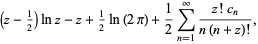 |
(10) |
where 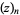 is a Pochhammer symbol,
is a Pochhammer symbol, 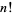 is a factorial, and
is a factorial, and
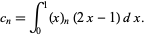 |
(11) |
The first few values of 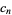 are
are
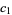 |
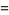 |
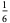 |
(12) |
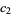 |
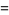 |
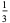 |
(13) |
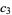 |
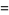 |
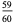 |
(14) |
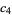 |
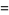 |
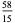 |
(15) |
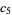 |
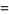 |
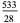 |
(16) |
(OEIS A054379 and A054380; Whittaker and Watson 1990, p. 253). Note that Whittaker and Watson incorrectly give 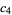 as 227/60.
as 227/60.
Yet another related result gives
![ln[Gamma(z)]=(z-1/2)lnz-z+1/2ln(2pi)+1/2[1/(2·3)sum_(r=1)^infty1/((z+r)^2)+2/(3·4)sum_(r=1)^infty1/((z+r)^3)+3/(4·5)sum_(r=1)^infty1/((z+r)^4)+...]
=(z-1/2)lnz-z+1/2ln(2pi)+1/2sum_(n=2)^infty((n-1))/(n(n+1))zeta(n,z+1)
=(z-1/2)lnz-z+1/2ln(2pi)+1/2sum_(n=2)^infty((-1)^n(n-1))/((n+1)!)psi_(n-1)(z)](http://mathworld.wolfram.com/images/equations/LanczosApproximation/NumberedEquation7.gif) |
(17) |
(Whittaker and Watson 1990, p. 261), where 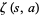 is a Hurwitz zeta function and
is a Hurwitz zeta function and 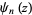 is a polygamma function.
is a polygamma function.
REFERENCES:
Lanczos, C. J. Soc. Indust. Appl. Math. Ser. B: Numer. Anal. 1, 86-96, 1964.
Luke, Y. L. "An Expansion for 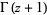 ." §2.10.3 in The Special Functions and their Approximations, Vol. 1. New York: Academic Press, pp. 29-31, 1969.
." §2.10.3 in The Special Functions and their Approximations, Vol. 1. New York: Academic Press, pp. 29-31, 1969.
Sloane, N. J. A. Sequences A054379 and A054379 in "The On-Line Encyclopedia of Integer Sequences."
Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990.



|
|
|
|
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
|
|
|
|
|
|
|
ممتص الصدمات: طريقة عمله وأهميته وأبرز علامات تلفه
|
|
|
|
|
|
|
المجمع العلمي للقرآن الكريم يقيم جلسة حوارية لطلبة جامعة الكوفة
|
|
|