المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Kei |
 1924
 01:57 مساءً
date: 25-3-2019 |
Author : Abramowitz, M. and Stegun, I. A. 
Book or Source : "Kelvin Functions." §9.9 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover 
Page and Part : ...|
Read More
Date: 12-9-2019
1184
Date: 29-9-2018
3120
Date: 24-3-2019
1759
|
The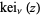 
function is defined as the imaginary part of
 |
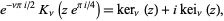(1) |
where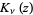 
is a modified Bessel function of the second kind. Therefore,
![kei_nu(z)=I[e^(-nupii/2)K_nu(ze^(pii/4))],](http://mathworld.wolfram.com/images/equations/Kei/NumberedEquation2.gif) |
(2) |
where ![I[z]](http://mathworld.wolfram.com/images/equations/Kei/Inline3.gif)
is the imaginary part.
It is implemented as KelvinKei[nu, z].
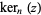has a complicated series given by Abramowitz and Stegun (1972, p. 380).
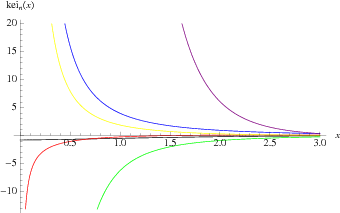
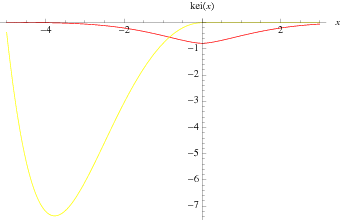
The special case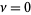 
is commonly denoted 
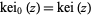and has the plot shown above.
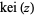has the series expansion
![kei(z)=-ln(1/2z)bei(z)-1/4piber(z)
+sum_(k=0)^infty(-1)^k(psi(2k+2))/([(2k+1)!]^2)(1/4z^2)^(2k+1),](http://mathworld.wolfram.com/images/equations/Kei/NumberedEquation3.gif) |
(3) |
where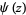 
is the digamma function (Abramowitz and Stegun 1972, p. 380).
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Kelvin Functions." §9.9 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 379-381, 1972.
Prudnikov, A. P.; Marichev, O. I.; and Brychkov, Yu. A. "The Kelvin Functions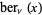 
, 
, 
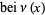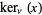and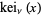 
." §1.7 in Integrals and Series, Vol. 3: More Special Functions. Newark, NJ: Gordon and Breach, pp. 29-30, 1990.
|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
المجمع العلمي يصدرُ مجموعةَ أبحاثٍ علميَّةٍ محكَّمةٍ في مجلَّة الذِّكرِ
|
|
|
