Only Critical Point in Town Test

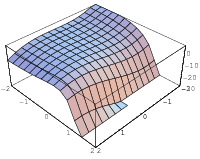
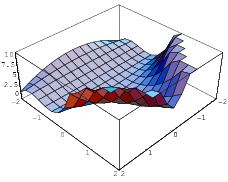
If a univariate real function 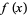 has a single critical point and that point is a local maximum, then  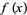has its global maximum there (Wagon 1991, p. 87). The test breaks downs for bivariate functions, but does hold for bivariate polynomials of degree 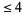. Such exceptions include

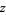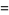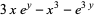			(1)
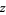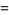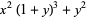			(2)
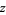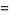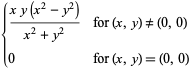			(3)

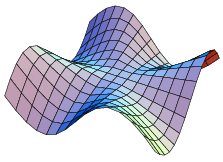
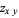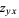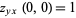(Rosenholtz and Smylie 1985, Wagon 1991). Note that equation (3) has discontinuous partial derivatives  and , and  and .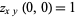

REFERENCES:

Anton, H. Calculus: A New Horizon, 6th ed. New York: Wiley, 1999.

Apostol, T. M.; Mugler, D. H.; Scott, D. R.; Sterrett, A. Jr.; and Watkins, A. E. A Century of Calculus, Part II: 1969-1991. Washington, DC: Math. Assoc. Amer., 1992.

Ash, A. M. and Sexton, H. "A Surface with One Local Minimum." Math. Mag. 58, 147-149, 1985.

Calvert, B. and Vamanamurthy, M. K. "Local and Global Extrema for Functions of Several Variables." J. Austral. Math. Soc. 29, 362-368, 1980.

Davies, R. "Solution to Problem 1235." Math. Mag. 61, 59, 1988.

Rosenholtz, I. and Smylie, L. "The Only Critical Point in Town Test." Math. Mag. 58, 149-150, 1985.

Wagon, S. "Failure of the Only-Critical-Point-in-Town Test." §3.4 in Mathematica in Action. New York: W. H. Freeman, pp. 87-91 and 228, 1991.