المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Inverse Erfc |
 1637
 05:08 مساءً
date: 21-8-2018 |
Author : Bergeron, F.; Labelle, G.; and Leroux, P 
Book or Source : Ch. 5 in Combinatorial Species and Tree-Like Structures. Cambridge, England: Cambridge University Press, 1998. 
Page and Part : ...|
Read More
Date: 8-9-2019
1492
Date: 10-5-2018
1309
Date: 23-7-2019
1135
|
The inverse erf function is the inverse function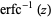 
of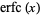 
such that
 |
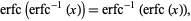(1) |
with the first identity holding for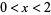 
and the second for 
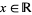. It is implemented in the Wolfram Language as InverseErfc[z].
It is related to inverse erf by
 |
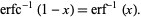(2) |
It has the special values
 |
 |
 |
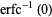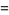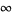(3) |
 |
 |
 |
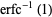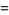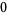(4) |
 |
 |
 |
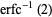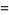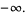(5) |
It has the derivative
![d/(dx)erfc^(-1)(x)=-1/2sqrt(pi)e^([erfc^(-1)(x)]^2),](http://mathworld.wolfram.com/images/equations/InverseErfc/NumberedEquation3.gif) |
(6) |
and its indefinite integral is
![interfc^(-1)(x)dx=(e^(-[erfc^(-1)(x)]^2))/(sqrt(pi))](http://mathworld.wolfram.com/images/equations/InverseErfc/NumberedEquation4.gif) |
(7) |
(which follows from the method of Parker 1955).
The Taylor series about 1 is given by
 |
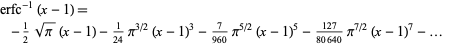(8) |
(OEIS A002067 and A007019).
REFERENCES:
Bergeron, F.; Labelle, G.; and Leroux, P. Ch. 5 in Combinatorial Species and Tree-Like Structures. Cambridge, England: Cambridge University Press, 1998.
Carlitz, L. "The Inverse of the Error Function." Pacific J. Math. 13, 459-470, 1963.
Parker, F. D. "Integrals of Inverse Functions." Amer. Math. Monthly 62, 439-440, 1955.
Sloane, N. J. A. Sequences A002067/M4458, A007019/M3126, A092676, and A092677 in "The On-Line Encyclopedia of Integer Sequences."
|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|
