


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 21-7-2018
Date: 13-7-2018
Date: 23-7-2018
|
The partial differential equation
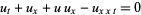 |
(Benjamin et al. 1972; Arvin and Goldstein 1985; Zwillinger 1997, p. 130). A generalized version is given by
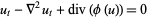 |
(Goldstein and Wichnoski 1980; Zwillinger 1997, p. 132).
REFERENCES:
Arvin, J. and Goldstein, J. A. "Global Existence for the Benjamin-Bona-Mahony Equation in Arbitrary Dimensions." Nonlinear Anal. 9, 861-865, 1985.
Benjamin, T. B.; Bona, J. L.; and Mahony, J. J. "Model Equations for Long Waves in Nonlinear Dispersive Systems." Philos. Trans. Roy. Soc. London Ser. A 272, 47-48, 1972.
Goldstein, J. A. and Wichnoski, B. J. "On the Benjamin-Bona-Mahony Equation in Higher Dimensions." Nonlinear Anal. 4, 665-675, 1980.
Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, pp. 130 and 132, 1997.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|